Tree, Binary search tree
03 Dec 2020 -
4 minute read
- Tree
- 트리의 Time Complextity
- JS> Tree 메소드 구현
- Binary Search Tree
- 이진 탐색 트리의 탐색
- 이진 탐색 트리의 종류
- 이진 탐색 트리의 Time Complexity
- JS> Binary Search Tree 메소드 구현
Tree
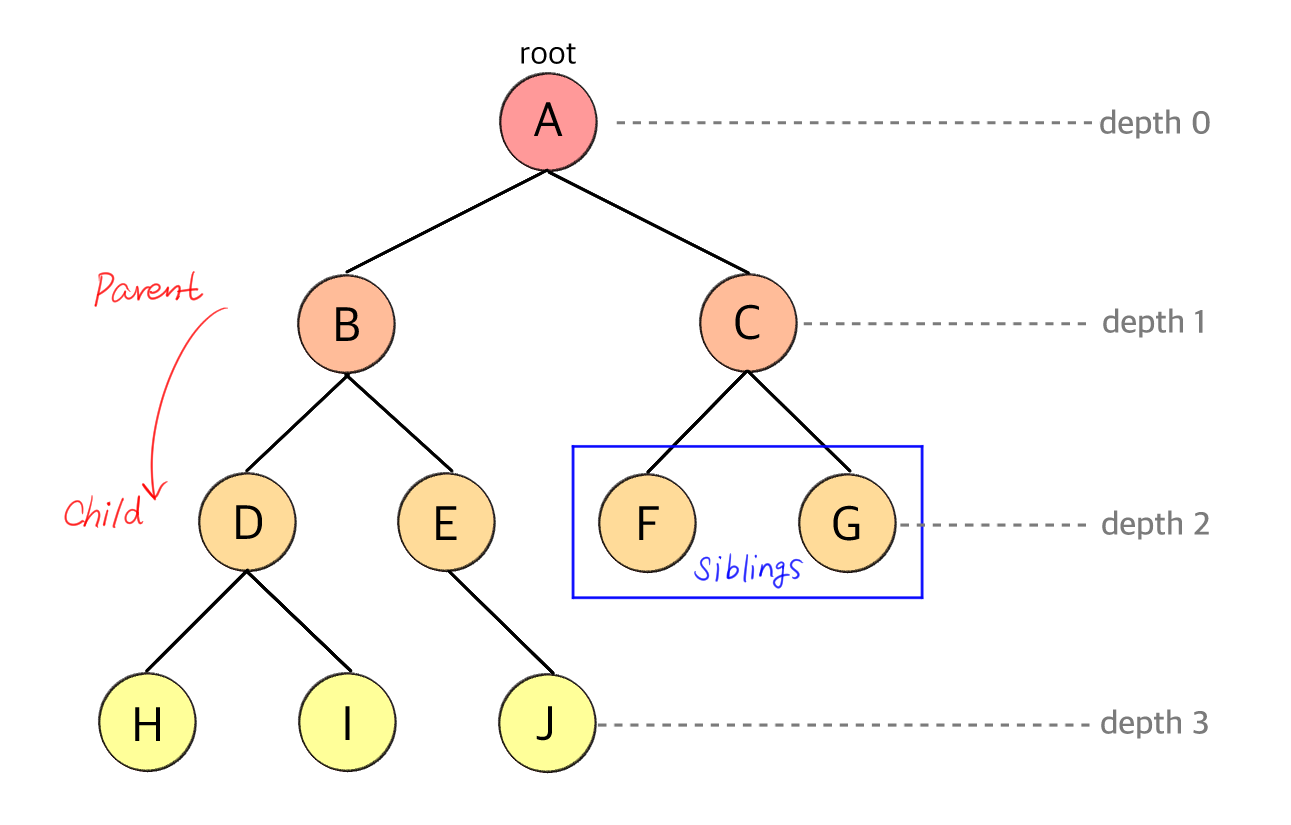
- 노드로 구성된 계층적인 자료구조
- 최상위 노드(root)를 만들고, 밑에 child를 추가하고, 그 밑에 또 child를 추가하는 방식으로 tree 구조를 구현한다.
- depth: 루트를 기준으로, 다른 노드로 접근하기 위한 거리 // D의 깊이 2
- level: 트리의 특정 깊이를 가지는 노드의 집합 // A의 레벨 1, B와 C의 레벨 2
- 노드의 차수(degree): 하위 트리 갯수(각 노드가 지닌 가지의 수) // A의 차수 2, B의 차수 2, E의 차수 1
- 트리의 차수: 트리의 최대 차수 // A, B, C, D에서의 차수가 트리의 최대 차수(2)
- 트리의 높이(height): 루트 노드에서 가장 깊숙이 있는 노드의 깊이 // 3
- 노드의 크기: 자신을 포함한 모든 자손의 갯수 / B의 크기 6
- 같은 부모를 가지면서 같은 depth에 존재하는 노드들을 sibling 관계에 있다.
- A는 B와 C의 부모(parent)
- B와 C는 A의 자식(child)
- 노드와 노드를 잇는 선: edge
- 자식이 없는 노드: leaf
트리의 Time Complextity
- N 링크 표현법: 하나의 노드는 최대 N개의 자식을 가지며 그 자식 또한 최대 N개의 자식을 가진다.
- 모든 노드의 총 갯수는 m개
탐색
- 모든 노드를 탐색해야하기 때문에 최악의 경우 O(m)의 시간 복잡도를 갖는다.
노드 삽입
- 자식 노드의 마지막에 삽입 => O(1)의 시간 복잡도
노드 삭제
- 원하는 노드를 찾기 위해 최악의 경우 모든 노드를 탐색해야 한다. 따라서 O(m)의 시간 복잡도를 갖는다.
JS> Tree 메소드 구현
class TreeNode {
constructor(value) {
this.value = value;
this.children = [];
}
insertNode(value) {
this.children.push(new TreeNode(value))
}
contains(value) {
// 방법 1
let result = false;
let inner = function(obj) {
if (obj.value === value) {
result = true;
}
obj.children.forEach(function(child) {
inner(child)
})
}
inner(this)
return result;
// 방법 2
if (this.value === value) {
return true;
}
for (let i = 0; i < this.children.length; i += 1) {
const childNode = this.children[i];
if (childNode.contains(value)) {
return true;
}
}
return false;
}
}
Binary Search Tree
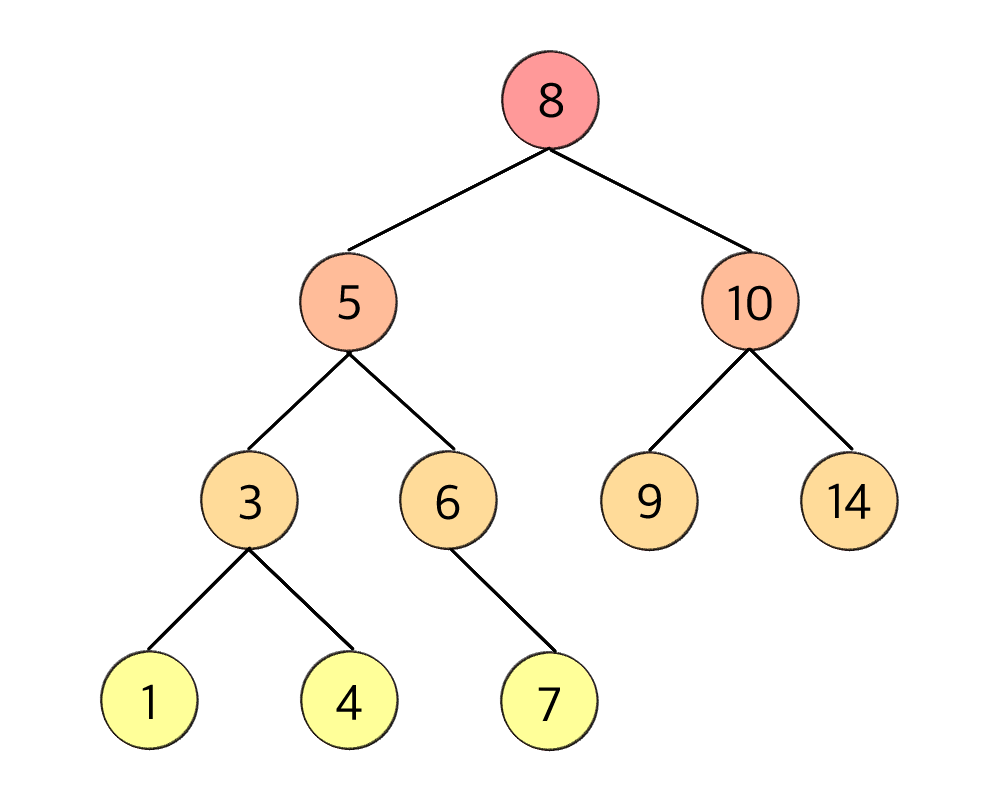
- 각 노드가 최대 2개의 자식만 갖는 트리
- 노드의 값이 정렬 방법에 따라 순서가 존재한다.
- 노드의 왼쪽(left) 서브트리에는 노드의 값보다 작은 값이, 오른쪽(right) 서브트리에는 노드의 값보다 같거나 큰 값이 저장된다.
- 자식이 한 개일 때도 적용된다. 위치가 다를 경우 다른 이진 트리이다.
이진 탐색 트리의 탐색
- 전위 순회(Preorder Traversal): 부모 -> 좌 -> 우
- 중위 순회(Inorder Traversal): 좌 -> 부모 -> 우
- 후위 순회(Postorder Traversal): 좌 -> 우 -> 부모
이진 탐색 트리의 종류
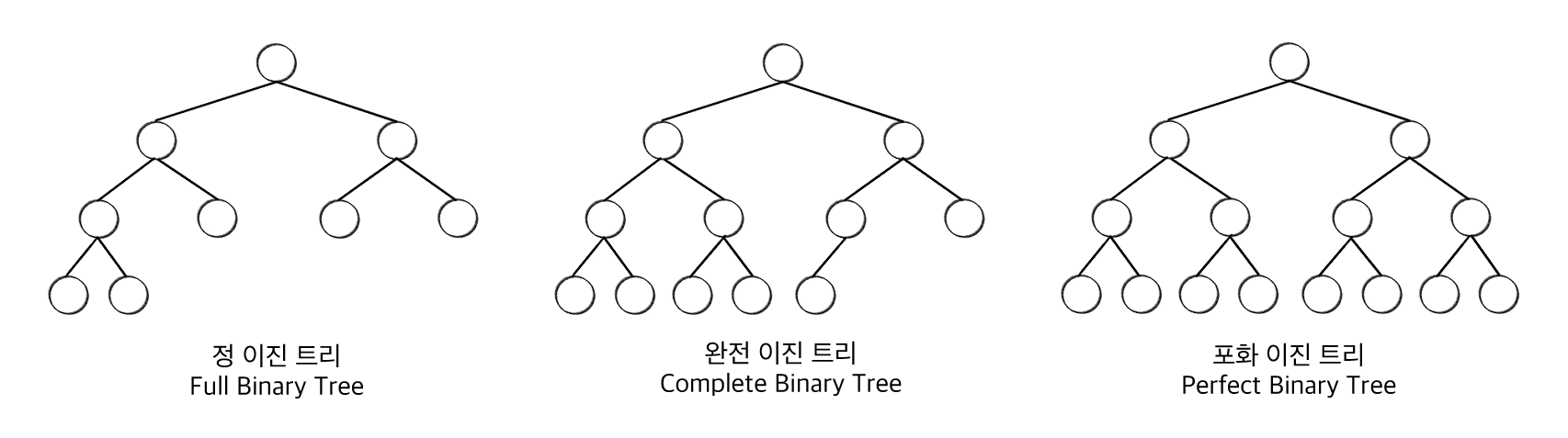
- 정 이진 트리(Full binary tree): 각 내부 노드가 두 개의 자식 노드를 갖는 순서화된 트리. 홀수 개의 자식 노드를 가질 수 없다.
- 완전 이진 트리(Complete binary tree): 부모, 왼쪽 자식, 오른쪽 자식 순으로 채워지는 트리
- 마지막 레벨을 제외하고 모든 노드가 가득 차 있어야 한다.
- 마지막 레벨의 노드도 중간에 빈 곳 없이 왼쪽으로 몰려 있어야 한다.
- 포화 이진 트리(Perfect binary tree): 모든 leaf node의 레벨이 동일하며, 모든 레벨이 가득 찬 트리
- 힙(Heap): 부모 자식 간의 대소관계는 정의되어 있으나(부모>자식) sibling의 대소관계(좌?우)는 정의되지 않은 트리
이진 탐색 트리의 Time Complexity
- 높이가 h인 포화 이진 트리는 (2^h - 1)개의 노드를 갖는다.
- 노드가 N개인 포화 혹은 완전 이진트리의 높이는 log N
- 노드가 N개일 때 최악의 경우 높이는 N // 편향 트리
탐색
- 값에 따라 왼쪽 서브트리 혹은 오른쪽 서브트리를 재귀적으로 탐색한다.
- 때문에 트리의 높이(height)만큼, 즉 O(h)의 시간복잡도를 갖는다.
- 최대 O(log n)으로 탐색할 수 있다.
노드 삽입
- 값이 root보다 작을 경우 왼쪽, 클 경우 오른쪽, 다시 그 자식보다 작을 경우 왼쪽, 클 경우 오른쪽으로 내려가면서 삽입할 위치를 찾는다.
- 트리의 높이만큼의 시간 복잡도를 갖는다. / O(h)
노드 삭제
- leaf 노드일 경우(자식이 없는 경우) 탐색 후 바로 삭제 가능하므로 O(h)
- 자식 노드가 하나일 경우 탐색 및 삭제 후 자식 노드가 해당 삭제된 위치로 올라가도록 연결하는 작업(삭제 노드의 자식노드와 부모노드를 연결)이 추가로 필요하다.
- 자식 노드가 두개일 경우 삭제 후 다시 트리를 만들어주는 작업이 필요하다.
- 삭제 노드보다 크면서(오른쪽 서브트리) 최소값(successor)을 찾아 삭제 위치에 복사해둔 후, 기존 위치 successor를 삭제한다.
- successor는 이진 탐색 트리의 구조상 왼쪽 자식은 갖지 않기 때문에(오른쪽 서브트리의 최소값이므로) 오른쪽 서브트리 위치에 자식 노드를 하나 가지거나 가지지 않는다.
- 따라서 successor의 삭제는 leaf 노드일 경우나 자식 노드가 하나일 경우에 맞춰 삭제된다.
JS> Binary Search Tree 메소드 구현
class BinarySearchTreeNode {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
insert(value) {
if (value < this.value) {
if (this.left === null) {
this.left = new BinarySearchTreeNode(value)
} else {
this.left.insert(value)
}
} else if (value > this.value) {
if (this.right === null) {
this.right = new BinarySearchTreeNode(value)
} else {
this.right.insert(value)
}
}
}
contains(value) {
if (this.value === value) {
return true;
} else if (value < this.value && this.left) {
return this.left.contains(value)
} else if (value > this.value && this.right) {
return this.right.contains(value)
}
return false;
}
inorder(callback) {
if (this.left) {
this.left.inorder(callback)
}
callback(this.value)
if (this.right) {
this.right.inorder(callback)
}
}
}