Hash Table
03 Dec 2020 -
3 minute read
Hash Table
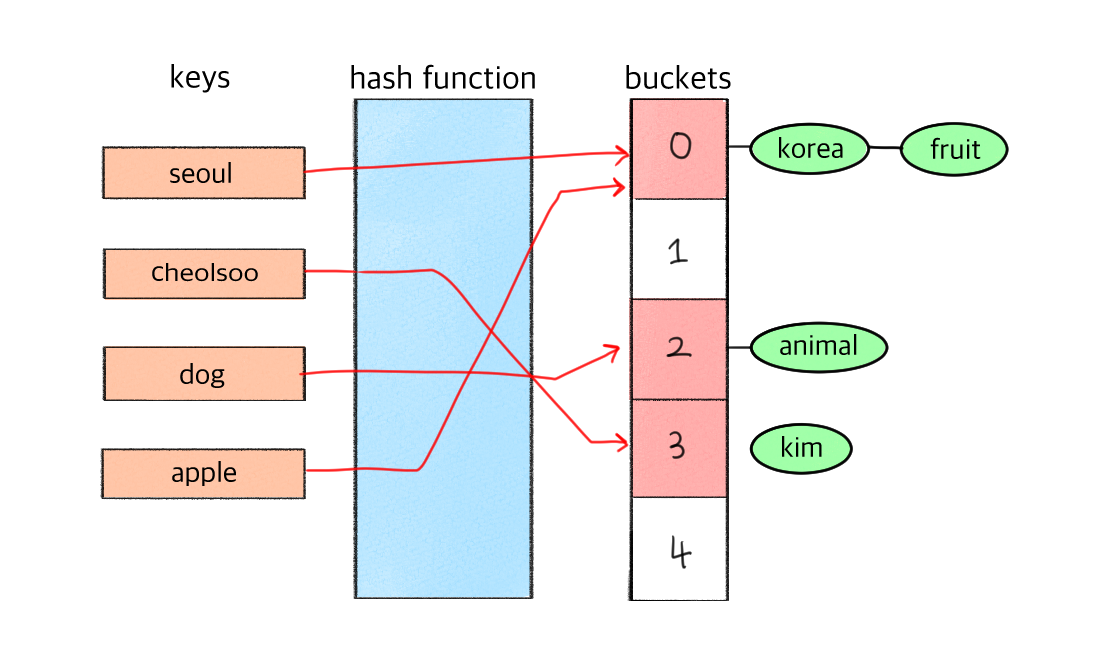
- key와 value를 매핑하는 자료구조 // 두 가지 데이터(키: 값)를 연결시켜주는 자료구조
- hash function을 통해 큰 값이나 정수가 아닌 key도 작은 범위의 인덱스에 매핑할 수 있다.
- key를 저장할 때 메모리 공간을 덜 사용할 수 있도록 해쉬함수를 통해 인덱스값으로 변환하는 것
- key값이 해쉬 함수를 거쳐서 해쉬 코드를 할당받고, 해쉬 코드가 bucket(value를 저장할 배열)의 인덱스 값을 가리킨다. 이 인덱스 주소에 key와 연결된 value를 저장한다.
F(key) -> Hash Code -> index -> value
hash function
- 항상 bucket의 크기 내의 결과값을 산출해야 한다.
- 같은 키를 넣었을 때 항상 같은 값이 나와야 한다.
- 어떠한 저장 없이 값을 주면 값을 내줘야 한다.
collision
- 서로 다른 key가 같은 index를 배정받았을 경우 충돌이 일어난다.
- 충돌을 해결하는 두 가지 방법이 있다.
1. Closed Addressing(separate chaining)
- 각 index가 linked list를 가리키고, linked list에 데이터들이 비연속적으로 연결된다.
- 동일 index를 가지는 데이터 간의 충돌이 일어나면 index가 가리키는 linked list에 데이터 노드를 추가하여 충돌을 해결할 수 있다.
- linked list만큼의 추가적인 메모리를 사용한다.
2. Open Addressing
- 추가적인 메모리 공간의 사용 없이 bucket의 빈 공간을 사용한다.
- linear probing: 해당 인덱스에 다른 데이터가 이미 저장되어 있으면 bucket에서 고정폭만큼씩 이동하면서 비어있는 bucket을 찾아 데이터를 저장한다. 탐색 시에는 해당 인덱스에 일치하는 key값이 없을 경우 다음 인덱스를 검색해 나가면서 같은 key가 나올때까지, key가 없을 때까지 검색한다.
- 중간의 데이터가 삭제처리 되었을 시 뒤의 데이터를 이어서 검색하기가 어렵다. 때문에 데이터를 삭제한 후 그 자리에 dummy node를 삽입하여 다음 index까지 검색이 연결되도록 해줘야 한다.
Time Complexity
- 기본적으로 chaining 방식이 많이 쓰이기 때문에, chaining의 시간 복잡도를 따져본다.
탐색
- bucket의 총 크기를 m, 들어가는 key의 갯수를 n이라고 할 때, 한 칸의 bucket에 들어가는 key의 평균 갯수는 n/m = α, 즉 인덱스 하나의 linked list의 평균 길이가 α.
- key값을 해쉬 코드로 매핑하는 데 O(1)의 시간이 들고, 최악의 경우 α 길이 linked list의 tail에 데이터가 있다면 α개의 데이터를 모두 탐색해야 한다. 따라서 최악의 경우 O(1 + α)의 시간 복잡도가 든다.
- 해당 key에 해당하는 value가 없을 경우에도 끝까지 탐색해야하기 때문에 O(1 + α)의 시간 복잡도를 가질 것이다.
노드 삽입
- key에 해쉬 코드를 할당하는 데 O(1), linked list에 데이터를 추가하는 작업 O(1)의 시간이 필요하므로 총 O(1)의 상수 시간 복잡도를 갖는다.
노드 삭제
- key값을 해쉬 코드로 매핑하는 데 O(1), 해당 bucket을 탐색하는 데 최악의 경우 O(α)의 시간이 든다. 탐색 후 삭제 연산은 비교적 작기 때문에 무시 가능하다.
resizing
- 최선의 시간 복잡도를 유지하기 위해 공간을 효율적으로 사용해야 한다.
- hash table은 25% ~ 75%가 차있을 때 효과적이다.
- bucket이 차있는 비율이 75%를 넘어가면 bucket을 2배 늘려준다.
- bucket이 25%보다 덜 찬 경우 bucket의 사이즈를 반 줄인다.
JS> Hash Table 메소드 구현
class HashTable {
constructor() {
this._size = 0;
this._bucketNum = 8;
this._storage = LimitedArray(this._bucketNum);
}
insert(key, value) {
const index = hashFunction(key, this._bucketNum);
const bucket = this._storage.get(index) || [];
for (let i = 0; i < bucket.length; i += 1) {
const tuple = bucket[i];
if (tuple[0] === key) {
const oldValue = tuple[1];
tuple[1] = value;
return oldValue;
}
}
bucket.push([key, value]);
this._storage.set(index, bucket);
this._size += 1;
if (this._size > this._bucketNum * 0.75) {
this._bucketNum *= 2
this._resize(this._bucketNum)
}
return undefined;
}
retrieve(key) {
const index = hashFunction(key, this._bucketNum);
const bucket = this._storage.get(index) || [];
for (let i = 0; i < bucket.length; i += 1) {
const tuple = bucket[i];
if (tuple[0] === key) {
return tuple[1];
}
}
return undefined;
}
remove(key) {
const index = hashFunction(key, this._bucketNum);
const bucket = this._storage.get(index) || [];
for (let i = 0; i < bucket.length; i += 1) {
const tuple = bucket[i];
if (tuple[0] === key) {
bucket.splice(i, 1);
this._size -= 1;
if (this._size < this._bucketNum * 0.25) {
this._bucketNum = Math.floor(this._bucketNum * 0.5)
this._resize(this._bucketNum);
}
return tuple[1];
}
}
return undefined;
}
_resize(newBucketNum) {
const oldStorage = this._storage;
newBucketNum = Math.max(newBucketNum, 8);
if (newBucketNum === this._bucketNum) {
return;
}
this._bucketNum = newBucketNum;
this._storage = LimitedArray(this._bucketNum);
this._size = 0;
oldStorage.each((bucket) => {
if (!bucket) {
return;
}
for (let i = 0; i < bucket.length; i += 1) {
const tuple = bucket[i];
this.insert(tuple[0], tuple[1]);
}
});
}
}